Chers lecteurs, en cette saison de joie et de magie, laissez-moi vous transporter dans un monde où les probabilités rencontrent la féerie de Noël. Imaginez-vous au matin de Noël, les yeux brillants d’excitation, devant trois mystérieux paquets au pied du sapin. Étiquetés A, B et C, ces paquets vous intriguent : l’un d’entre eux contient le cadeau que vous espériez tant, tandis que les deux autres, malicieusement préparés par les lutins, sont vides.
Vous pointez d’une main tremblante vers le paquet A. Soudain, un bruit de grelots se fait entendre et, dans un tourbillon de neige scintillante, apparaît le Père Noël en personne ! Avec un clin d’œil malicieux, il soulève le paquet C, révélant son contenu vide, puis vous demande d’une voix joviale : « Veux-tu changer ton choix et essayer le paquet B ? »
Votre cœur balance. Garder le A ou switcher pour le B ? Cela ressemble à un dilemme à 50/50, n’est-ce pas ? Mais accrochez vos guirlandes, car voici un twist digne d’un conte de Noël !

En réalité, suivre les conseils du Père Noël et changer votre choix pour le paquet B augmente vos chances de dénicher le précieux cadeau. Au départ, en choisissant le paquet A, vous aviez une chance sur trois de réussir. En éliminant un paquet vide, le Père Noël vous indique subtilement que si votre choix initial était erroné (ce qui est probable à deux chances sur trois), le vrai cadeau se trouve maintenant dans l’autre paquet restant.
« Attendez une seconde », vous exclamez en dégustant un morceau de pain d’épice. « Cela défie toute logique ! » Et pourtant, c’est là que la magie des probabilités et la sagesse du Père Noël brillent. Cette situation illustre comment l’IA, avec son approche basée sur les probabilités et la réévaluation constante, peut nous guider vers des décisions plus éclairées, même si elles semblent contre-intuitives.
Ce Noël, osez penser différemment. Lorsque de nouvelles informations viennent éclairer votre chemin, n’hésitez pas à réévaluer vos choix. Après tout, dans l’esprit des fêtes, un changement de perspective pourrait bien vous conduire au cadeau de vos rêves.
Joyeux Noël à tous, et que l’esprit de Noël vous guide dans vos propres énigmes de la vie. Rappelez-vous, un petit changement de stratégie inspiré par le Père Noël (ou un lutin !) peut faire toute la différence entre un paquet vide et une merveilleuse surprise sous le sapin.
Le problème de Monty Hall
Ce problème est connu sous le nom de Monty Hall, quelques explications avec les probabilité conditionnelles
- Premier choix : Lorsque vous choisissez un paquet parmi les trois (A, B, C), il y a une chance sur trois (33,33%) que vous choisissiez le bon paquet et deux chances sur trois (66,67%) que le bon paquet soit parmi ceux que vous n’avez pas choisis.
- Élimination d’un paquet : Lorsqu’un paquet vide est retiré des deux non choisis, si votre choix initial était incorrect (ce qui se produit dans 66,67% des cas), le seul autre paquet restant doit contenir le cadeau. Si votre choix initial était correct (33,33% des cas), le cadeau est toujours dans votre paquet initial.
- Changement de choix : En changeant de choix, vous gagnez si votre choix initial était incorrect, ce qui arrive dans 66,67% des cas. Si vous ne changez pas, vous ne gagnez que si votre choix initial était correct, ce qui arrive dans 33,33% des cas.
D’où vient le problème de Mont Hall ?

L’origine du Problème de Monty Hall remonte à un jeu télévisé américain nommé « Let’s Make a Deal », animé par Monty Hall dans les années 1960 et 1970. Le jeu comprenait une séquence où un candidat devait choisir entre trois portes, derrière l’une desquelles se trouvait un prix de valeur (comme une voiture), et derrière les deux autres, des lots de consolation moins désirables (souvent humoristiquement appelés « Zonks », qui pouvaient être des chèvres ou d’autres objets sans valeur).
Après que le candidat ait fait son choix initial, Monty Hall ouvrait l’une des deux portes restantes qu’il savait contenir un lot de consolation, puis demandait au candidat s’il souhaitait changer son choix pour l’autre porte fermée. Cette situation est à la base du célèbre problème de probabilité.
Le problème a été popularisé dans un plus large public par un article de Marilyn vos Savant dans sa colonne « Ask Marilyn » du magazine « Parade » en 1990. Elle a expliqué pourquoi il était mathématiquement avantageux de changer de choix, ce qui a déclenché un débat public étendu, avec de nombreuses personnes, y compris des universitaires, contestant initialement sa réponse avant qu’elle ne soit largement acceptée comme correcte.
Vous trouverez plus de détail sur la page wikipedia
Mais pourquoi avons nous tant de peine avec les probalités conditionnelles ?
Disons que le cerveau humain aime simplifier les problèmes et dans ce cas cela engendre des biais cognitifs :
- Biais de la probabilité équi-probable : Les gens supposent souvent, à tort, que dans une situation où plusieurs résultats semblent possibles, ces résultats sont également probables (par exemple, penser que chaque paquet restant a une chance égale de contenir le cadeau).
- Biais de statu quo ou Biais d’ancrage : Il y a une tendance naturelle à maintenir une décision initiale ou un choix initial (le premier paquet choisi), même lorsque de nouvelles informations devraient inciter à changer de décision. C’est la tendance à s’accrocher trop fortement à une première information (le premier choix de paquet) et à ne pas ajuster suffisamment cette perception lorsque des informations supplémentaires sont fournies.
- Biais de représentativité : Cela se produit quand les gens jugent la probabilité d’un événement en se basant sur la manière dont il se représente dans leur esprit, plutôt que sur les statistiques réelles.
Comment réagissent les intelligences artificielles face à ce problème ?
Pour explorer la compréhension des probabilités par les intelligences artificielles, j’ai récemment posé le célèbre Problème de Monty Hall à deux systèmes d’IA renommés : Bard de Google et ChatGPT-4 d’OpenAI.
Bard, n’a pas réussi à déjouer l’intuition humaine typique. Lorsqu’il a été confronté au dilemme de savoir s’il fallait changer de choix après l’élimination d’une option non gagnante, Bard a répondu qu’il y avait 50% de chances de réussir, reflétant ainsi l’erreur commune faite par de nombreuses personnes.
En revanche, ChatGPT-4 a brillamment démontré sa compréhension des subtilités du problème. Il a correctement identifié que changer de choix augmentait les chances de gagner à environ 66,67%, illustrant ainsi une maîtrise remarquable des principes de probabilité conditionnelle et de réévaluation des décisions.
Ce résultat souligne non seulement la sophistication de ChatGPT-4 en matière de raisonnement probabiliste, mais aussi la variété des compétences et des approches au sein des différents modèles d’IA.
Toujours pas convaincu ?
Dans ce cas, je vous propose de le prouver par l’experimentation avec un petit programme en python reproduisant ce problème.
Voici le résultat, après 10000 éxécutions, le résultat est sans appel !
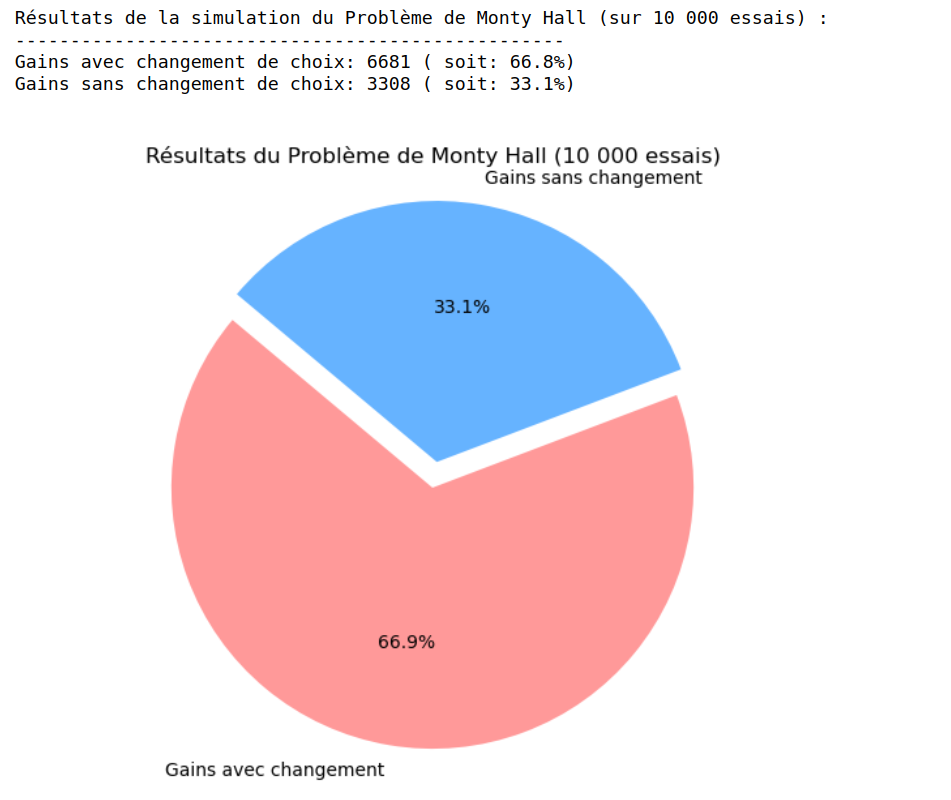
Et voici le programme python du problème de Monty hall
Et pour ceux qui doutent encore ou les plus courageux d’entre vous, je vous laisse le code du programme pour que vous puissez l’executer sur votre PC:
import random
import matplotlib.pyplot as plt
def monty_hall(change_choice: bool) -> bool:
"""
Simulation du Problème de Monty Hall.
Args:
change_choice (bool): Indique si le joueur change de choix après que le père noël (alias Monty) ait révélé un paquet vide.
Returns:
bool: True si le joueur gagne, False sinon.
"""
# Les paquets sont numérotés 0, 1, 2.
cadeau = random.randint(0, 2)
# Le joueur fait un choix initial.
choix_joueur = random.randint(0, 2)
# Le père noël élimine un paquet qui n'est ni le choix du joueur, ni celui avec le cadeau.
paquets_possibles = [0, 1, 2]
paquets_possibles.remove(choix_joueur)
if cadeau in paquets_possibles:
paquets_possibles.remove(cadeau)
paquet_éliminé = random.choice(paquets_possibles)
# Le joueur change de choix s'il a choisi cette option.
if change_choice:
paquets_restants = [0, 1, 2]
paquets_restants.remove(choix_joueur)
paquets_restants.remove(paquet_éliminé)
choix_joueur = paquets_restants[0]
# Le joueur gagne s'il a choisi le paquet avec le cadeau.
return choix_joueur == cadeau
# Simulation de 10 000 essais.
nb_essais = 10000
gains_changement = sum(monty_hall(True) for _ in range(nb_essais))
gains_sans_changement = sum(monty_hall(False) for _ in range(nb_essais))
pourcentage_avec_changement = gains_changement / nb_essais * 100
pourcentage_sans_changement = gains_sans_changement / nb_essais * 100
# Formatage des résultats
resultat = (
f"Résultats de la simulation du Problème de Monty Hall (sur 10 000 essais) :\n"
f"--------------------------------------------------\n"
f"Gains avec changement de choix: {gains_changement} ( soit: {pourcentage_avec_changement:.1f}%)\n"
f"Gains sans changement de choix: {gains_sans_changement} ( soit: {pourcentage_sans_changement:.1f}%)\n"
)
print(resultat)
# Préparation des données pour le diagramme
labels = 'Gains avec changement', 'Gains sans changement'
sizes = [pourcentage_avec_changement, pourcentage_sans_changement]
colors = ['#ff9999','#66b3ff']
explode = (0.1, 0) # "explode" le premier morceau
# Création du diagramme
plt.figure(figsize=(8, 6))
plt.pie(sizes, explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', startangle=140)
plt.axis('equal') # Assure que le pie est dessiné comme un cercle.
# Affichage du diagramme
plt.title('Résultats du Problème de Monty Hall (10 000 essais)')
plt.show()
